The littleendian function
The definitions below can be found in LittleEndian.hs and the testing code can be found in Test_LittleEndian.hs.
Inputs and Outputs
To quote Bernstein: If b is a 4-byte sequence then littleendian(b) is a word, and, hence, its Haskell type is:
littleendian :: Quad (W 8) -> W 32 -- i.e., (W 8, W 8, W 8, W 8) -> W 32
Bernstein also notes that littleendian is invertible, meaning that the following function can be defined:
inv_littleendian :: W 32 -> Quad (W 8)
Definition
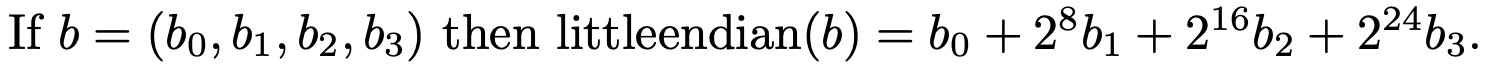
Rendering in ReWire/Haskell
Note that the (++) operator below is vector concatenation (rather than list append from the Haskell prelude). So, in the definition of littleendian below, four (W 8) bit vectors (i.e., b3, b2, b1, and b0) are concatenated to make a single (W 32).
revbytes :: Quad (W 8) -> Quad (W 8)
revbytes (b0,b1,b2,b3) = (b3,b2,b1,b0)
littleendian :: Quad (W 8) -> W 32
littleendian w8x4 = b3 ++ b2 ++ b1 ++ b0
where
b0 , b1 , b2 , b3 :: W 8
(b3 , b2 , b1 , b0) = revbytes w8x4
Bernstein also notes that littleendian is invertible:
inv_littleendian :: W 32 -> Quad (W 8)
inv_littleendian w = revbytes (slice0 w , slice1 w , slice2 w , slice3 w)
Here, the operation of the slice functions (slice0, etc.) is illustrated by the following test:
slicetest :: P.Bool
slicetest = (slice0 x , slice1 x , slice2 x , slice3 x) P.== (lit 0xde , lit 0xad , lit 0xbe , lit 0xef)
where
x :: W 32
x = lit 0xdeadbeef
These functions are defined in LittleEndian.hs and are uninteresting.
Examples

alltests :: [P.Bool]
alltests = [test1 , test2 , test3] P.++ invertible_tests
test1 , test2 , test3 :: P.Bool
test1 = littleendian (lit 0,lit 0,lit 0,lit 0) == lit 0x00000000
test2 = littleendian (lit 86,lit 75,lit 30,lit 9) == lit 0x091e4b56
test3 = littleendian (lit 255,lit 255,lit 255,lit 250) == lit 0xfaffffff
invertible_tests :: [P.Bool]
invertible_tests = [ invert q0 P.== q0
, invert q1 P.== q1
, invert q2 P.== q2
]
where
invert :: Quad (W 8) -> Quad (W 8)
invert q = inv_littleendian (littleendian q)
λ> slicetest
True
λ> alltests
[True,True,True,True,True,True]